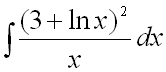 .
.В данном примере множитель
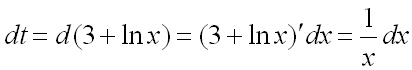 .
.Тогда:
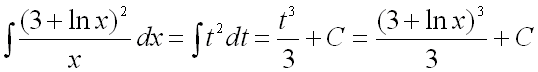 .
.Ответ:
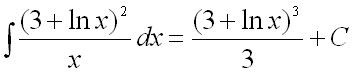 .
.Тема "Метод замены переменной (способ подстановки)"
Пример
1. Найти
неопределенный интеграл 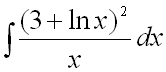 .
.
В данном примере множитель ![]() ,
стоящий под знаком интеграла, есть производная от выражения
,
стоящий под знаком интеграла, есть производная от выражения ![]() ,
стоящего в числителе, следовательно, для нахождения интеграла воспользуемся
заменой:
,
стоящего в числителе, следовательно, для нахождения интеграла воспользуемся
заменой:
![]() ,
,
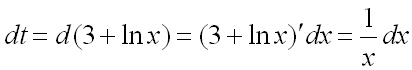 .
.
Тогда:
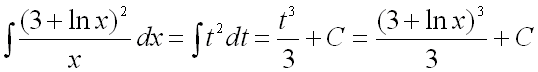 .
.
Ответ: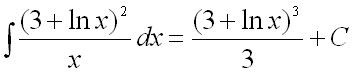 .
.
Пример 2. Найти неопределенный интеграл ![]() .
.
В данном примере подынтегральная функция содержит два полинома ![]() и
и ![]() ,
второй степени и третей степени соответственно. Легко проверить, что первый
полином есть, с точностью до константы, производная от второго полинома:
,
второй степени и третей степени соответственно. Легко проверить, что первый
полином есть, с точностью до константы, производная от второго полинома:
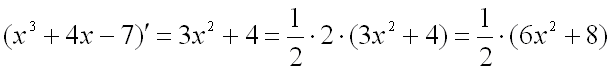 .
.
Следовательно, для нахождения интеграла воспользуемся заменой:
![]() ,
,
![]() ;
;
умножим левую и правую части последнего равенства на 2:
![]() .
.
Тогда:
![]() .
.
Ответ:
![]() .
.
Пример 3.
Найти неопределенный интеграл 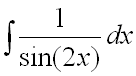 .
.
Прежде чем применить метод замены переменной, преобразуем подынтегральную функцию,
используя формулу для синуса двойного аргумента ![]() и правила тождественных преобразований:
и правила тождественных преобразований:
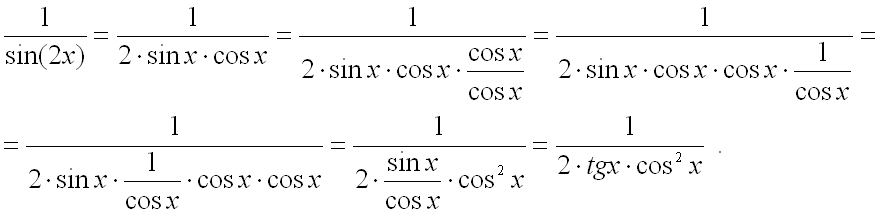
Теперь можно увидеть, что множитель 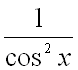 есть производная от
есть производная от ![]() ,
следовательно, для нахождения интеграла воспользуемся заменой:
,
следовательно, для нахождения интеграла воспользуемся заменой:
![]() ,
,
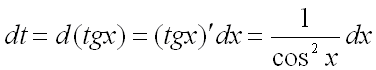 .
.
Тогда:
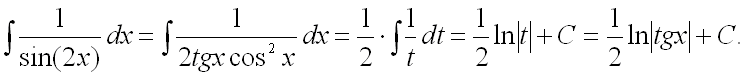
Ответ: 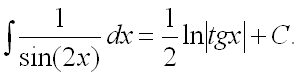
Пример 4.
Найти неопределенный интеграл 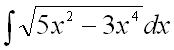 .
.
Прежде чем применить метод замены переменной, преобразуем подынтегральную функцию.
Вынесем в подкоренном выражении общий множитель ![]() за скобки, а затем и из-под корня:
за скобки, а затем и из-под корня:
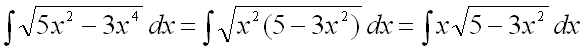 .
.
Поскольку множитель ![]() ,
стоящий под интегралом, есть, с точностью до константы, производная от выражения
,
стоящий под интегралом, есть, с точностью до константы, производная от выражения
![]() ,
то для нахождения интеграла воспользуемся заменой:
,
то для нахождения интеграла воспользуемся заменой:
![]() ,
,
![]() ;
;
умножим левую и правую части последнего равенства на ![]() :
:
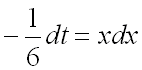 .
.
Тогда:
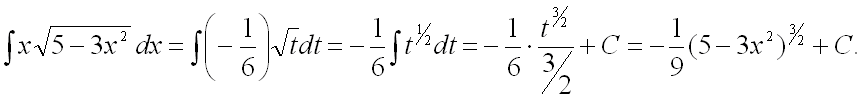
Ответ: 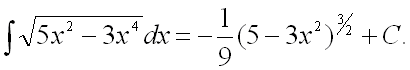
Пример 5.
Найти неопределенный интеграл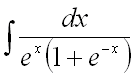 .
.
Прежде чем применить метод замены переменной, преобразуем подынтегральную функцию:
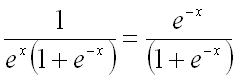 .
.
Теперь легко увидеть, что числитель ![]() есть, с точностью до константы, производная от знаменателя
есть, с точностью до константы, производная от знаменателя ![]() :
:
![]() .
.
Следовательно, для нахождения интеграла воспользуемся заменой:
![]() ,
,
![]() ;
;
умножим левую и правую части последнего равенства на (–1):
![]() .
.
Тогда:
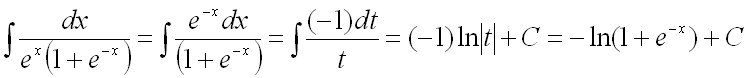 .
.
Ответ:
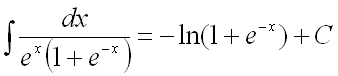 .
.
Пример 6.
Найти неопределенный интеграл 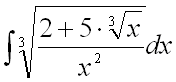 .
.
Для того чтобы применить метод замены переменной, предварительно преобразуем
подынтегральную функцию, используя понятие степени с дробным показателем и свойства
арифметических корней:
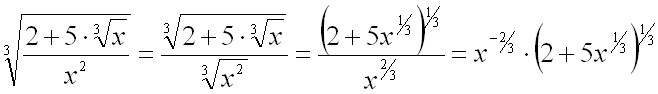 .
.
Теперь можно увидеть, что множитель ![]() является, с точностью до константы, производной от выражения
является, с точностью до константы, производной от выражения ![]() :
:
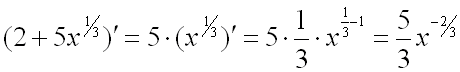 .
.
Следовательно, для нахождения интеграла воспользуемся заменой:
![]() ,
,
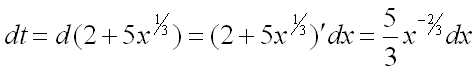 ;
;
умножим левую и правую части последнего равенства на ![]() :
:
 .
.
Тогда:
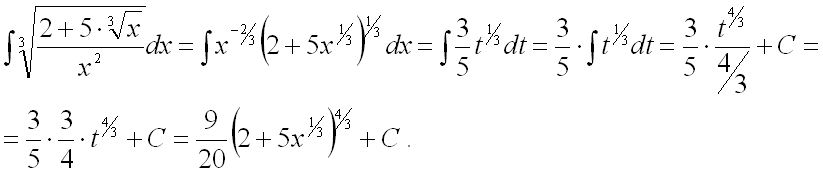
Ответ:
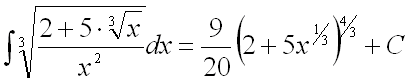 .
.
Пример 7.
Найти неопределенный интеграл 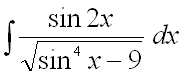 .
.
Для нахождения данного интеграла сначала разложим числитель подынтегральной
функции по формуле синуса двойного угла ![]() ,
а затем используем замену:
,
а затем используем замену:
![]() ,
,
![]() .
.
В результате получим:
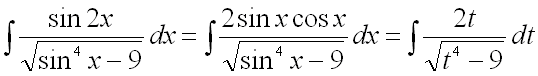 .
.
Для то чтобы привести последний интеграл к табличному, необходимо еще раз применить
метод замены переменной. В данном случае числитель подынтегральной функции ![]() есть производная от выражения
есть производная от выражения ![]() ,
поэтому делаем замену:
,
поэтому делаем замену:
![]() ,
,
![]() .
.
Тогда, делая вторую замену и в конце возвращаясь к исходной переменной, получим:
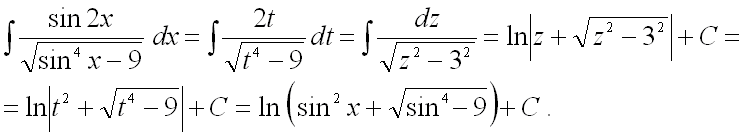
Замечание: данный ответ мог быть также получен и более
коротким способом с помощью только одной замены ![]() ,
,
![]() .
.
Ответ:
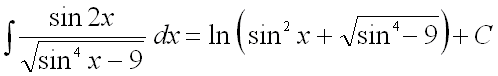 .
.