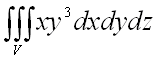Тема "Тройные интегралы"

Примеры решения задач

Пример 1. Вычислить тройной интеграл 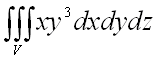, где область ограничена поверхностями , при этом .

Решение.

В данном примере область интегрирования ограничена сверху плоскостью , снизу – параболоидом вращения , вершина которого расположена в точке , а проекцией области на плоскость является область , расположенная в I четверти и ограниченная линиями: .
Для вычисления интеграла перейдем к цилиндрическим координатам:

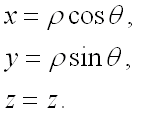
Модуль якобиана равен , а область интегрирования переходит в область , ограниченную поверхностями: .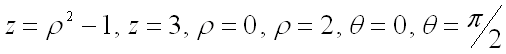
В результате перехода к цилиндрическим координатам и последующего сведения тройного интеграла к трехкратному получим:

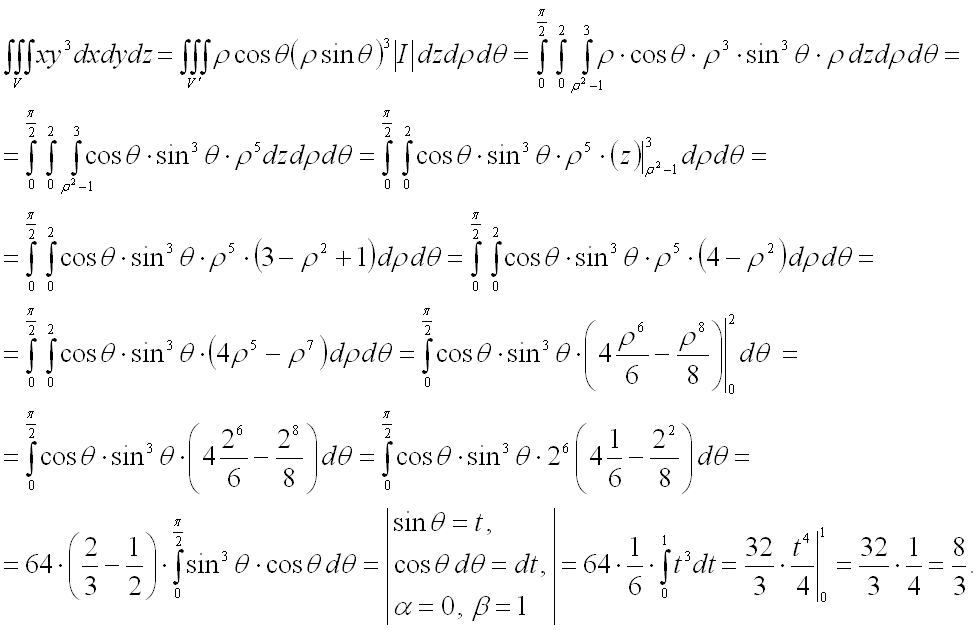
Ответ: .