Полный дифференциал функции нескольких переменных. Частные производные высших порядков

Частной производной по от функции называется предел отношения частного приращения этой функции по к приращению , когда последнее стремится к нулю:
.

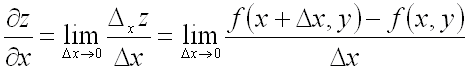Частной производной по от функции называется предел отношения частного приращения этой функции по к приращению , когда последнее стремится к нулю:
.

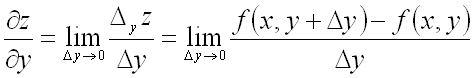Пусть задана функция . Если аргументу сообщить приращение , а аргументу – приращение , то функция получит приращение , которое называется полным приращением функции и определяется формулой: .

Функция , полное приращение которой в данной точке может быть представлено в виде суммы двух слагаемых (выражения, линейного относительно и , и величины бесконечно малой высшего порядка относительно ):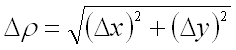
,
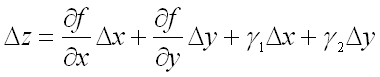где и стремятся к нулю, когда и стремятся к нулю (т.е. когда 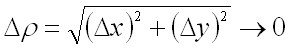), называется дифференцируемой в данной точке.

Линейная (относительно и ) часть полного приращения функции называется полным дифференциалом и обозначается :
,
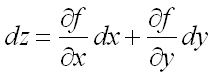где и – дифференциалы независимых переменных, которые, по определению, равны соответствующим приращениям и .

Частные производные от частных производных первого порядка называются частными производными второго порядка. Для функции двух переменных их четыре:

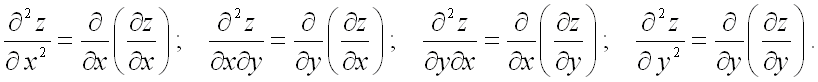
Примеры решения задач

Пример 1. Найти полный дифференциал функции .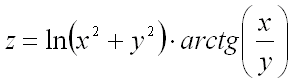

Решение.

Полным дифференциалом функции называется линейная (относительно и ) часть полного приращения функции: .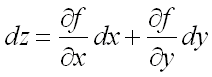

Следовательно, для выполнения задания достаточно найти частные производные первого порядка от функции и подставить их в вышеприведенную формулу.

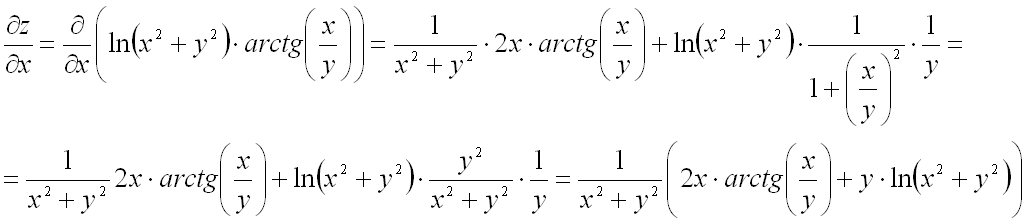
Здесь и ниже использовалось правило дифференцирования произведения двух функций и правило дифференцирования сложной функции одной переменной.

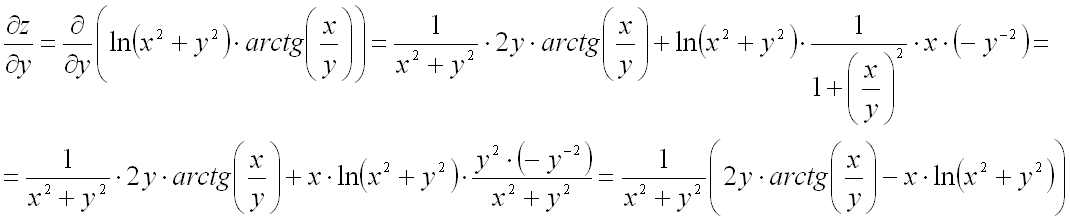
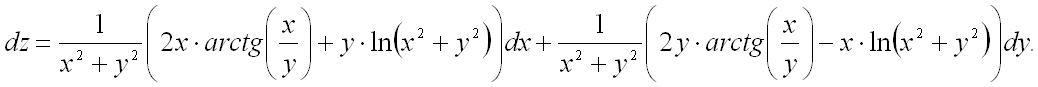
Ответ: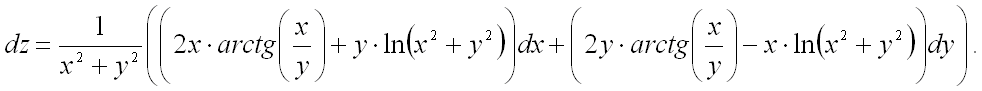