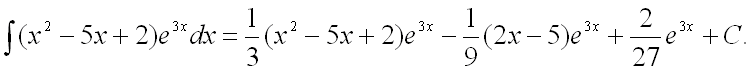Тема "Метод интегрирования по частям"

 

Пример 1. Найти неопределенный интеграл .
Используем формулу интегрирования по частям: , причем, поскольку под знаком интеграла стоит произведение полинома на натуральный логарифм, то в качестве функции необходимо взять , а в качестве – выражение . Кроме того, для применения формулы нужно найти значения и :
,
.
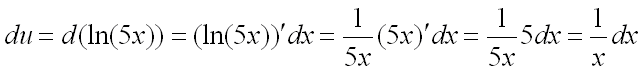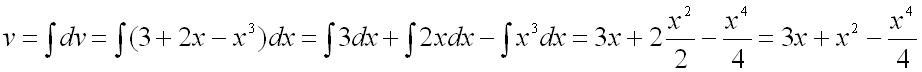Таким образом, получаем:

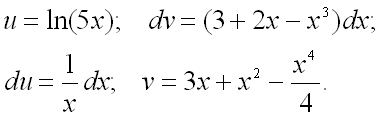
Следовательно,

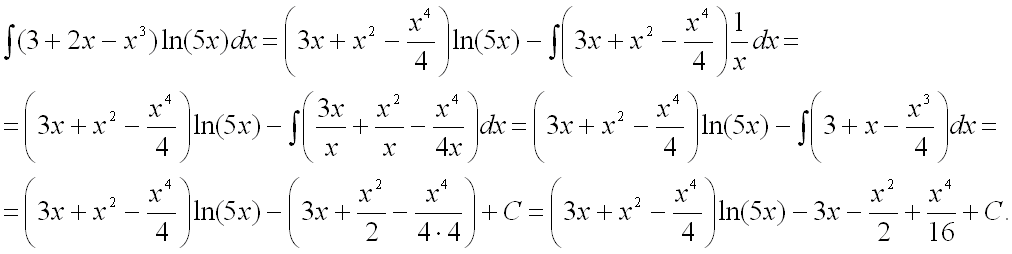
Ответ: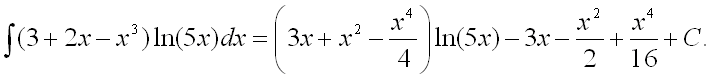

 

Пример 2. Найти неопределенный интеграл .
Используем формулу интегрирования по частям: , причем, поскольку под знаком интеграла стоит произведение полинома на обратную тригонометрическую функцию, то в качестве функции необходимо взять , а в качестве – выражение . Дополнительно найдем значения и :
,
.
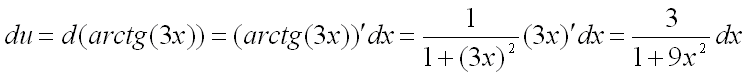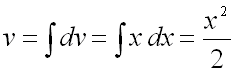Таким образом, получаем:

Следовательно,

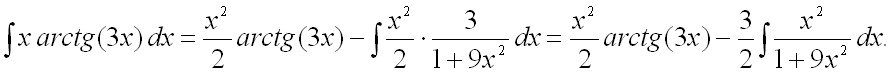
Найдем отдельно последний интеграл. Поскольку подынтегральная функция есть неправильная рациональная дробь (степень полинома в числителе больше или равна степени полинома в знаменателе), то сначала представим ее в виде суммы частного и остатка от деления (правильной рациональной дроби). В данном случае деление числителя на знаменатель проще производить не по правилу деления многочленов, а путем тождественных преобразований числителя. Затем каждый из полученных интегралов найдем на основе таблицы интегралов.

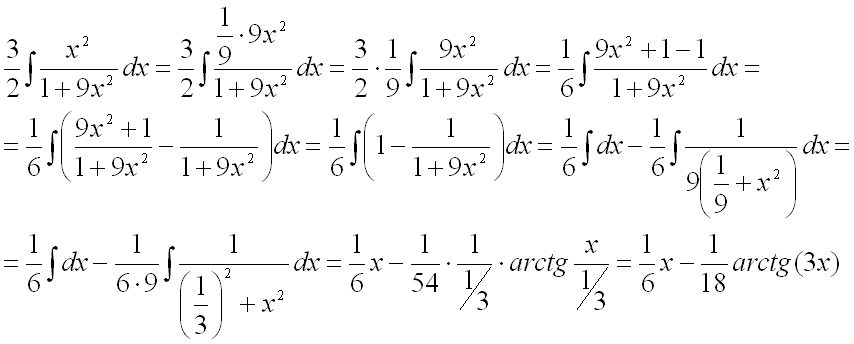
Подставим найденную первообразную в исходный интеграл:

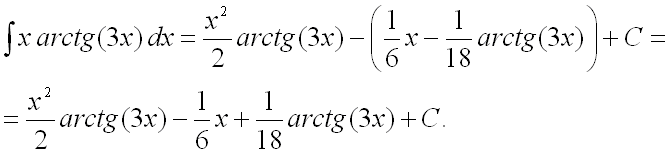
Ответ:

 

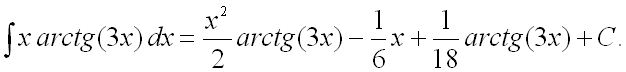
Пример 3. Найти неопределенный интеграл .
Используем формулу интегрирования по частям: , причем, поскольку под знаком интеграла стоит обратная тригонометрическая функция, то в качестве функции необходимо взять , а в качестве – выражение . Дополнительно найдем значения и :
,
.
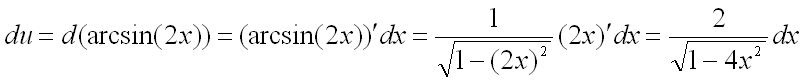Таким образом, получаем:

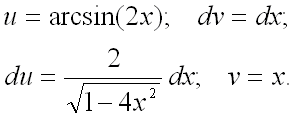
Следовательно,

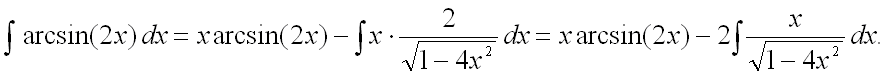
Найдем отдельно последний интеграл. Поскольку в числителе подынтегральной функции стоит (с точностью до постоянного множителя) производная от подкоренного выражения в знаменателе, то необходимо применить метод замены переменной. Положим , тогда . Выразим из последнего выражения и подставим все в последний интеграл:
,

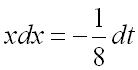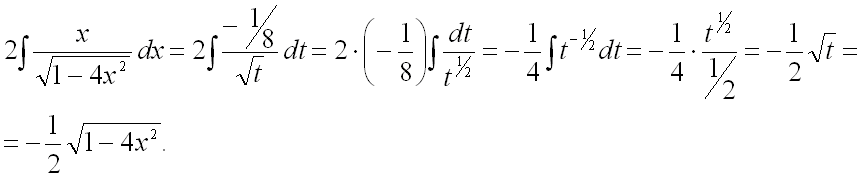
Подставим найденную первообразную в исходный интеграл:

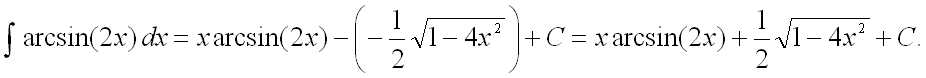
Ответ: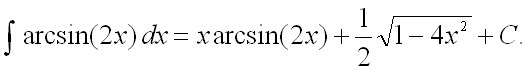

 

Пример 4. Найти неопределенный интеграл .
Используем формулу интегрирования по частям: , причем, поскольку под знаком интеграла стоит произведение полинома на тригонометрическую функцию , то в качестве функции необходимо взять полином , а в качестве – выражение . Кроме того, для применения формулы нужно найти значения и :
,
.
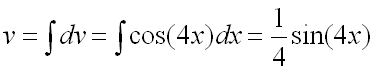При вычислении первообразной для последнего из интегралов можно воспользоваться методом замены переменной или правилом интегрирования: если , то .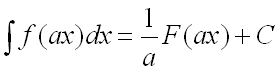
Таким образом, получаем:

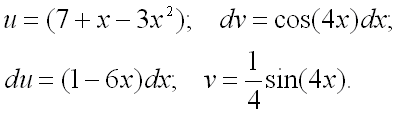
Следовательно,

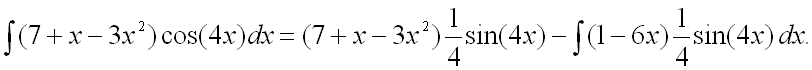
Для вычисления последнего интеграла еще раз воспользуемся методом интегрирования по частям. Теперь в качестве функции берется полином , а в качестве – выражение 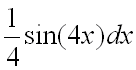. Найдем значения и :
,
.
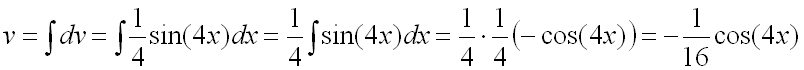Таким образом, получаем:

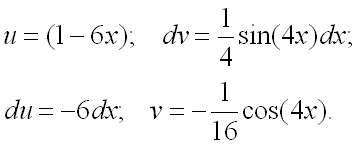
Следовательно,

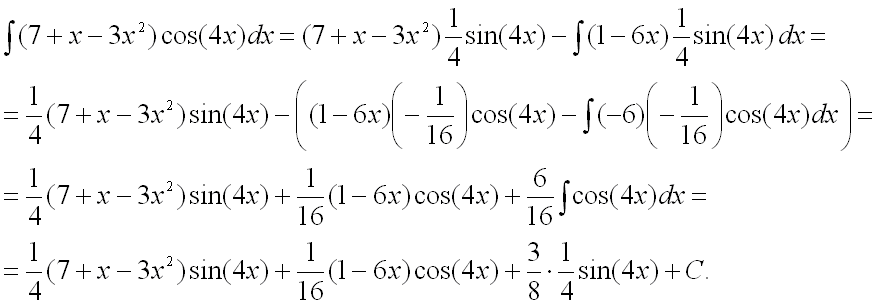
Ответ: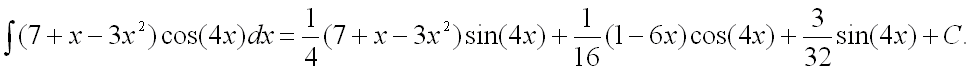

Пример 5. Найти неопределенный интеграл .
Используем формулу интегрирования по частям: , причем, поскольку под знаком интеграла стоит произведение полинома на функцию , то в качестве функции необходимо взять полином , а в качестве – выражение . Для того, чтобы применить формулу интегрирования по частям нужно дополнительно найти значения и :
,
.
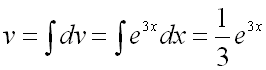При вычислении первообразной для последнего из интегралов можно воспользоваться методом замены переменной или правилом интегрирования: если , то .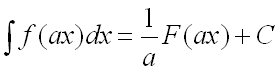
Таким образом, получаем:

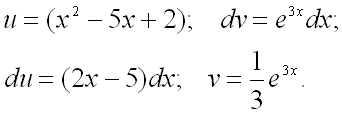
Следовательно,

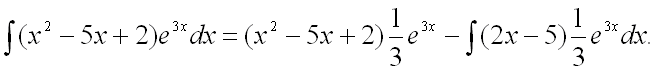
Для вычисления последнего интеграла еще раз воспользуемся методом интегрирования по частям. Теперь в качестве функции берется полином , а в качестве – выражение 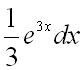. Найдем значения и :
,
.
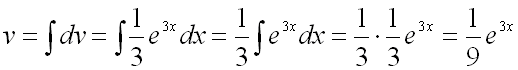Таким образом, получаем:

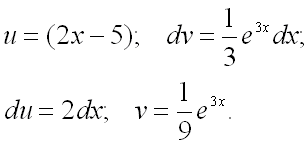
Следовательно,

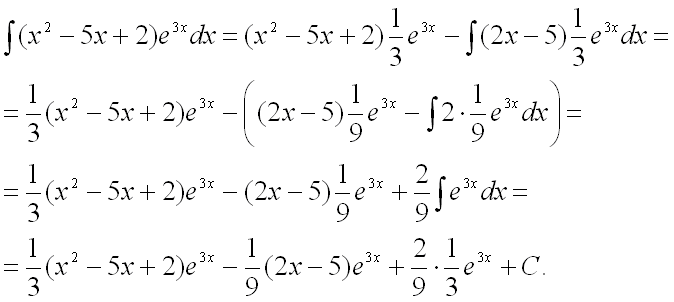
Ответ: