![]()
Производная по направлению. Градиент
Пусть в некоторой области
![]() задана функция
задана функция ![]() и точка
и точка ![]() .
Проведем из точки
.
Проведем из точки ![]() вектор
вектор ![]() ,
направляющие косинусы которого
,
направляющие косинусы которого ![]() .
На векторе
.
На векторе ![]() ,
на расстоянии
,
на расстоянии ![]() от его начала рассмотрим точку
от его начала рассмотрим точку ![]() ,
т.е.
,
т.е. 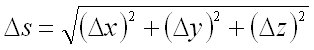 .
.
Будем предполагать, что функция ![]() и ее частные производные первого порядка непрерывны в области
и ее частные производные первого порядка непрерывны в области ![]() .
.
Предел отношения ![]() при
при ![]() называется
производной от функции
называется
производной от функции ![]() в точке
в точке ![]() по
направлению вектора
по
направлению вектора ![]() и обозначается
и обозначается ![]() ,
т.е.
,
т.е.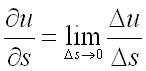 .
.
Для нахождения производной от функции![]() в заданной точке
в заданной точке ![]() по
направлению вектора
по
направлению вектора ![]() используют формулу:
используют формулу: 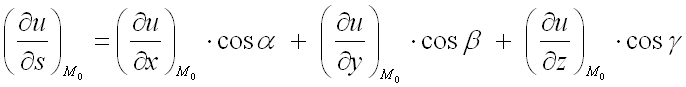 ,
,
где ![]() – направляющие косинусы вектора
– направляющие косинусы вектора ![]() ,
которые вычисляются по формулам:
,
которые вычисляются по формулам:
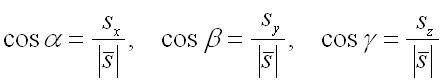 .
.
Пусть в каждой точке некоторой
области ![]() задана функция
задана функция ![]() .
.
Вектор, проекциями которого на оси координат являются значения частных производных
этой функции в соответствующей точке, называется градиентом функции
![]() и обозначается
и обозначается ![]() или
или ![]() (читается «набла у»):
(читается «набла у»): 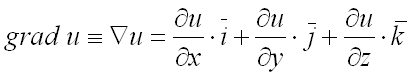 .
.
При этом говорят, что в области ![]() определено векторное поле градиентов.
определено векторное поле градиентов.
Для нахождения градиента функции ![]() в заданной точке
в заданной точке ![]() используют формулу:
используют формулу:
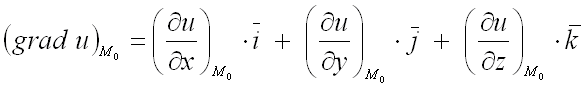 .
.
Свойства градиента
1. Производная
в данной точке по направлению вектора ![]() имеет наибольшее значение, если направление вектора
имеет наибольшее значение, если направление вектора ![]() совпадает с направлением градиента. Это наибольшее значение производной равно
совпадает с направлением градиента. Это наибольшее значение производной равно
![]() .
.
2. Производная
по направлению вектора, перпендикулярного к вектору ![]() ,
равна нулю.
,
равна нулю.
Примеры решения задач
Пример 1.
Найти производную от функции ![]() в точке
в точке ![]() по направлению вектора
по направлению вектора ![]() .
.
Решение.
Для решения задачи воспользуемся
формулой для нахождения производной от функции ![]() в заданной точке
в заданной точке ![]() по направлению вектора
по направлению вектора ![]() :
:
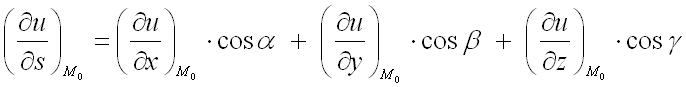 ,
,
где ![]() – направляющие косинусы вектора
– направляющие косинусы вектора ![]() ,
которые вычисляются по формулам:
,
которые вычисляются по формулам:
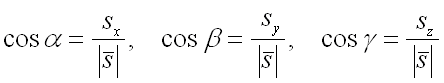 .
.
По условию задачи вектор ![]() имеет координаты
имеет координаты ![]() .
Тогда его длина равна:
.
Тогда его длина равна:
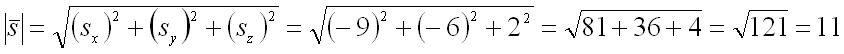 .
.
Следовательно, для направляющих косинусов вектора получим следующие значения:
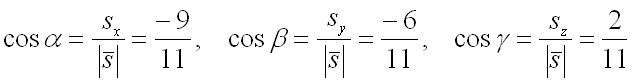 .
.
Далее для решения задачи необходимо найти все частные производные первого порядка
от функции ![]() :
:
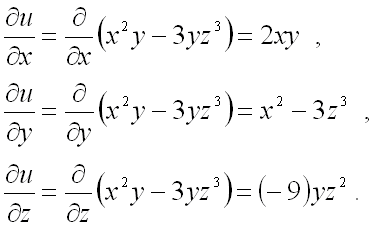
Вычислим значения этих частных производных первого порядка в точке ![]() :
:
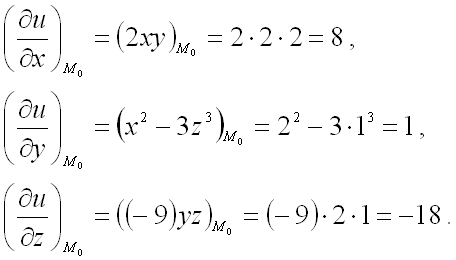
В заключении подставим полученные значения для направляющих косинусов вектора
![]() и значения частных производных первого порядка от функции
и значения частных производных первого порядка от функции ![]() в
точке
в
точке ![]() в формулу для нахождения производной по направлению в заданной точке:
в формулу для нахождения производной по направлению в заданной точке:
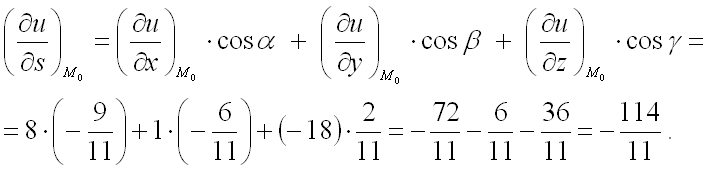
Ответ: производная от функции ![]() в точке
в точке ![]() по направлению вектора
по направлению вектора ![]() равна
равна 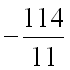 .
.
Пример 2.
Найти градиент функции 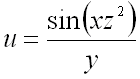 в точке
в точке 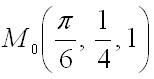 .
.
Решение.
Поскольку градиентом функции называется вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, то для решения задачи сначала найдем все частные производные первого порядка от заданной функции:
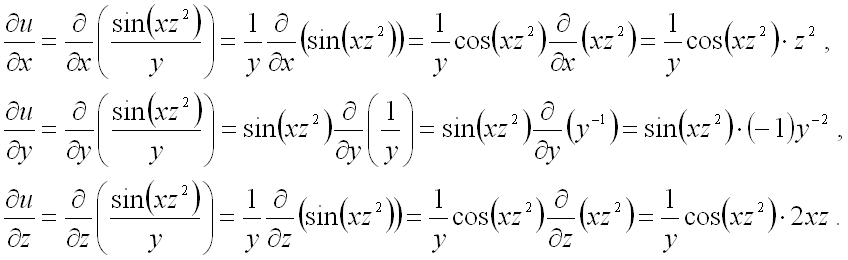
Далее вычислим значения этих частных производных первого порядка в точке 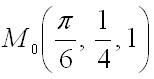 :
:
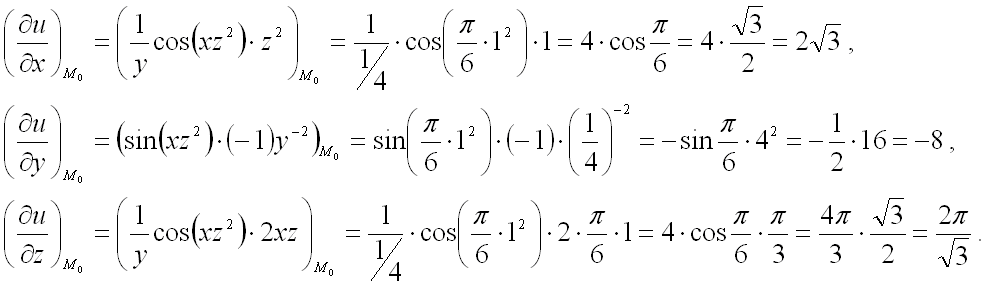
Подставим полученные значения в формулу градиента функции ![]() в заданной точке
в заданной точке ![]() :
:
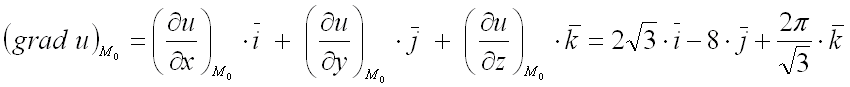 .
.
Ответ: градиент функции 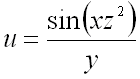 в точке
в точке 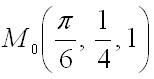 равен
равен 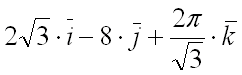 .
.
Пример 3.
Найти производную функции ![]() в точке
в точке 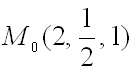 по направлению градиента функции
по направлению градиента функции ![]() в той же точке.
в той же точке.
Решение.
Для нахождения производной
от функции ![]() в заданной точке
в заданной точке ![]() по направлению вектора
по направлению вектора ![]() используют формулу:
используют формулу:
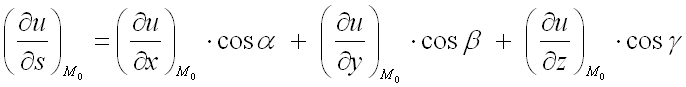 ,
,
где ![]() – направляющие косинусы вектора
– направляющие косинусы вектора ![]() ,
которые вычисляются по формулам:
,
которые вычисляются по формулам:
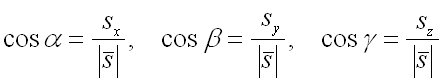 .
.
В данном случае вектор ![]() совпадает
с градиентом функции
совпадает
с градиентом функции ![]() в точке
в точке 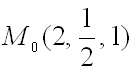 :
:
![]() .
.
Следовательно, для решения задачи необходимо найти значения всех частных производных
первого порядка от функции ![]() в точке
в точке ![]() ,
а также координаты и длину градиента функции
,
а также координаты и длину градиента функции ![]() в той же точке.
в той же точке.
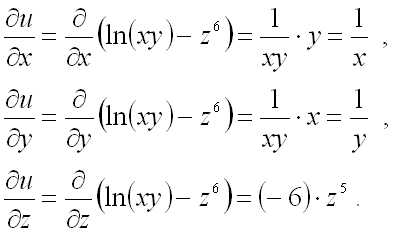
Вычислим значения частных производных первого порядка от функции ![]() в точке
в точке ![]() :
:
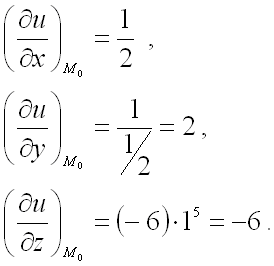
Для нахождения координат вектора ![]() ,
равного градиенту функции
,
равного градиенту функции ![]() в заданной точке
в заданной точке ![]() ,
вычислим значения частных производных первого порядка от функции
,
вычислим значения частных производных первого порядка от функции ![]() в этой точке:
в этой точке:
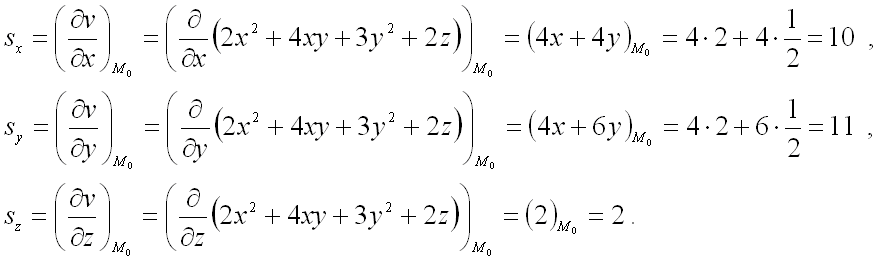
Длина вектора равна: 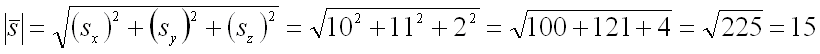 .
.
Найдем направляющие косинусы вектор по формулам:
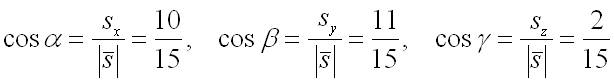 .
.
Подставим полученные значения в формулу для нахождения производной от функции
![]() в заданной точке
в заданной точке ![]() по направлению вектора
по направлению вектора ![]() :
:
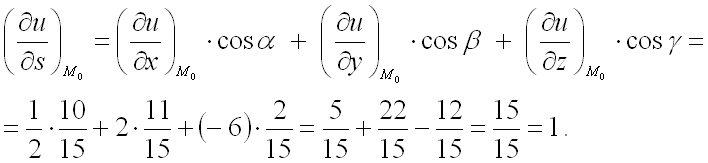
Ответ: производная функции ![]() в точке
в точке 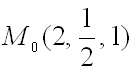 по
направлению градиента функции
по
направлению градиента функции ![]() в той же точке равна 1.
в той же точке равна 1.
Задания для самостоятельной работы
1.
Найти производную функции 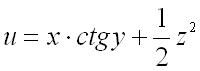 в точке
в точке 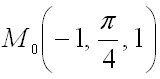 по направлению вектора
по направлению вектора ![]() .
.
Ответ: ![]() .
.
2. Найти производную функции ![]() в точке
в точке 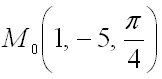 по направлению вектора
по направлению вектора ![]() .
.
Ответ: ![]() .
.
3. Найти производную функции ![]() в точке
в точке ![]() по направлению вектора
по направлению вектора ![]() .
.
Ответ: ![]() .
.
4. Найти градиент функции 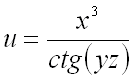 в точке
в точке 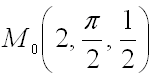 .
.
Ответ: ![]() .
.
5. Найти градиент функции 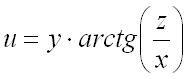 в точке
в точке ![]() .
.
Ответ: 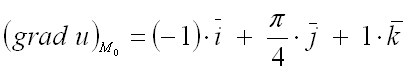 .
.
6. Найти градиент функции 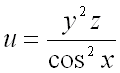 в точке
в точке 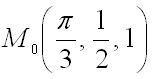 .
.
Ответ: ![]() .
.
![]()