Частные производные неявной функции нескольких переменных

Если в уравнении вида каждой паре чисел и из некоторой области соответствует одно или несколько значений , удовлетворяющих этому уравнению, то уравнение неявно определяет одну или несколько однозначных функций от и . В этом случае говорят, что есть неявная функция от и .

Частные производные и неявной функции находятся по формулам (предполагается, что ):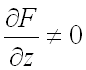
.

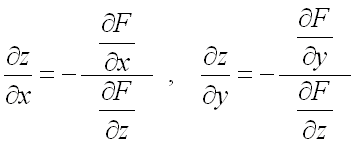Примеры решения задач

Пример 1. Найти частные производные первого порядка функции , заданной уравнением: .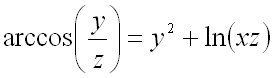

Решение.

Как известно, частные производные и неявной функции , заданной уравнением вида , находятся по формулам:
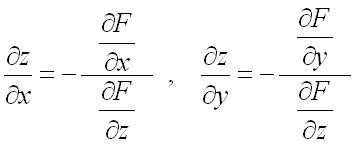, где предполагается, что .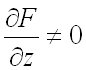

В нашем случае для решения задачи сначала необходимо преобразовать формулу, задающую функцию , к виду :
.

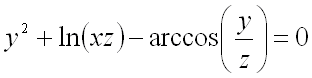Найдем частную производную :

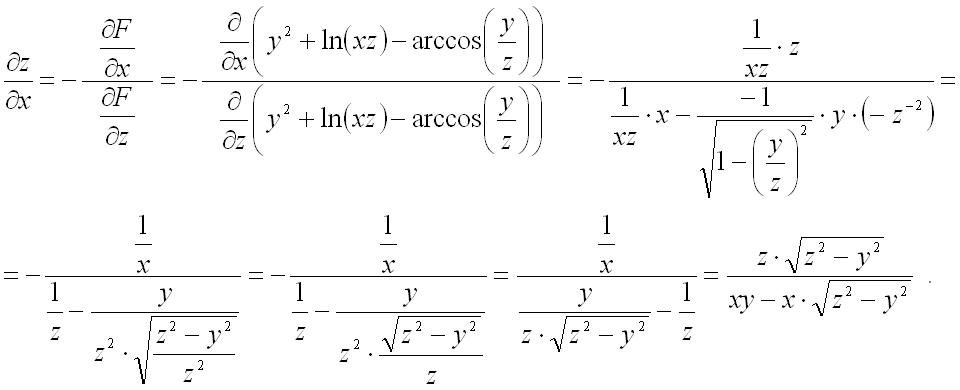
При вычислении второй частной производной первого порядка в знаменателе дроби сразу подставим результат, полученный для из первой частной производной с учетом смены знака:

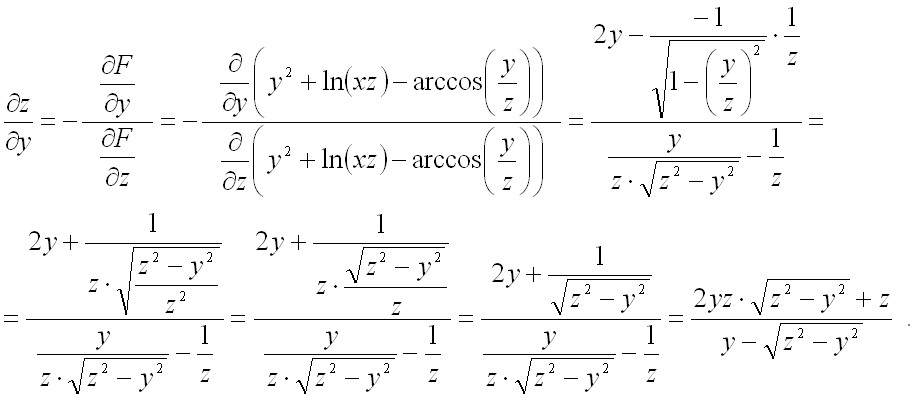
Ответ: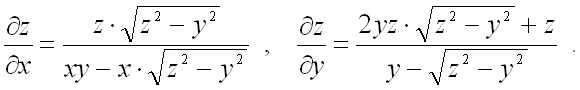