Частные производные сложной функции нескольких переменных

Предположим, что в уравнении и являются функциями независимых переменных и :
. В этом случае говорят, что есть сложная функция от аргументов и .

Если функции имеют непрерывные частные производные по всем своим аргументам, то
.

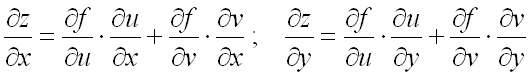Примеры решения задач

Пример 1. Найти и , если , где .

Решение.

Для отыскания частных производных сложной функции двух переменных воспользуемся формулами:

.

Найдем каждый из сомножителей, представленных в формуле:

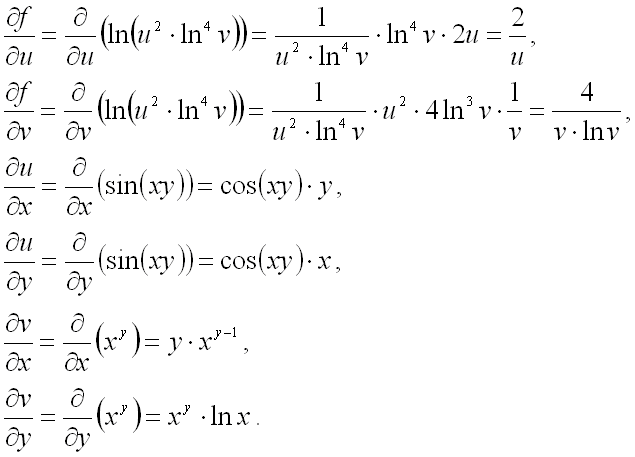
Подставим полученные выражения в формулы для нахождения частных производных сложной функции двух переменных:

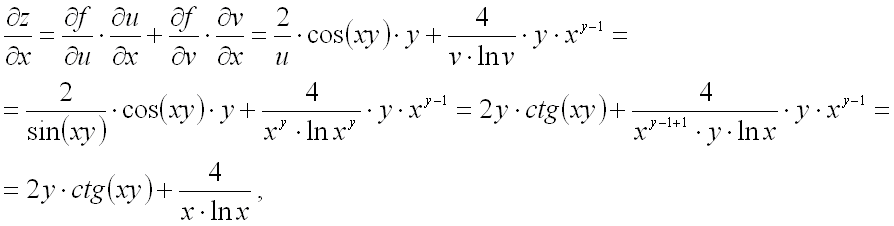
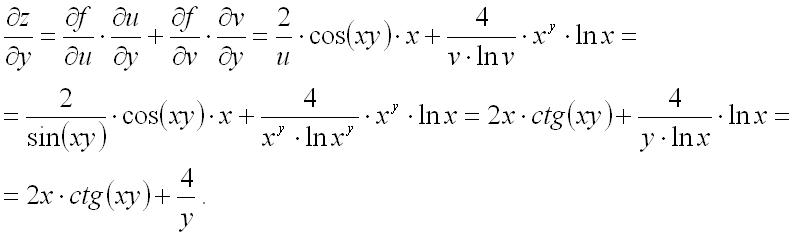
Ответ: 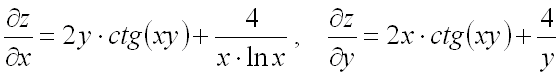.