Тема "Непрырывные случайные величины"

Функцией распределения вероятностей называют функцию , определяющую вероятность того, что случайная величина в результате испытания примет значение, меньшее , то есть:
.
Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Свойства функции распределения вероятностей случайной величины

1. Значения функции распределения вероятностей принадлежат отрезку :
.
2. Функция распределения вероятностей – неубывающая функция, то есть:
, если .
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале , равна приращению функции распределения вероятностей на этом интервале:
.
Следствие 2. Вероятность того, что непрерывная случайная величина примет одно определенное значение, равна нулю.
Используя последнее следствие, легко убедиться в справедливости следующих равенств:
.
3. Если возможные значения непрерывной случайной величины принадлежат интервалу , то:
, если ;
, если .
Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:
;
.
Плотностью распределения вероятностей непрерывной случайной величины называют функцию – первую производную от функции распределения вероятностей :
.
Таким образом, функция распределения вероятностей является первообразной для плотности распределения вероятностей.
Теорема. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу , равна определенному интегралу от плотности распределения, взятому в соответствующих пределах:
.
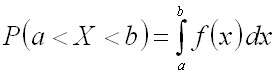Следовательно, зная плотность распределения вероятности , можно найти функцию распределения по формуле
.

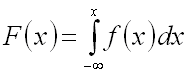Свойства плотности распределения вероятностей

1. Плотность распределения вероятностей – неотрицательная функция:
.
2. Несобственный интеграл от плотности распределения вероятностей в пределах от до равен единице:
.

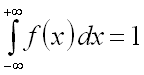Вероятностный смысл плотности распределения вероятности. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу , приближенно равна (с точностью до бесконечно малых высшего порядка относительно ) произведению плотности распределения вероятности в точке на длину интервала :
.

Числовые характеристики непрерывных случайных величин

Математическим ожиданием непрерывной случайной величины , возможные значения которой принадлежат отрезку , называют определенный интеграл
.
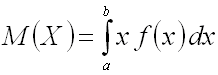Если возможные значения принадлежат всей числовой оси, то

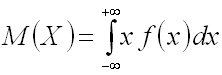
(предполагается, что несобственный интеграл, стоящий в правой части равенства, существует).
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Если возможные непрерывной случайной величины принадлежат отрезку , то
.
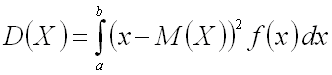Если возможные значения принадлежат всей числовой оси, то

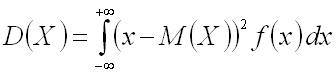
(предполагается, что несобственный интеграл, стоящий в правой части равенства, существует).
Средним квадратическим отклонением непрерывной случайной величины называют, как и для величины дискретной, квадратный корень из дисперсии:
.