Криволинейные интегралы

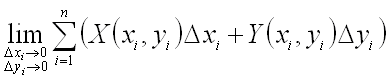Криволинейным интегралом II рода от функций и по плоской кривой от точки к точке называют предел , где точки – точки, которые разбивают участок кривой от точки до точки на частей, а и – приращения соответствующих координат при переходе от точки к точке . Криволинейный интеграл II рода обозначают:
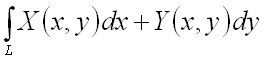или .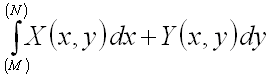
Направление по кривой от точки до точки называется направлением интегрирования.
Если кривая пространственная, то криволинейный интеграл II рода от трех функций , , определяется аналогично:

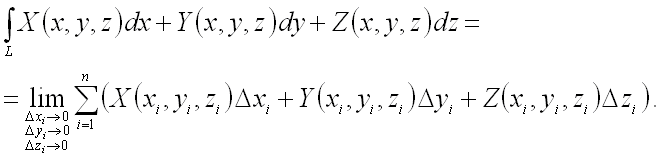
Свойства криволинейного интеграла II рода

1. Криволинейный интеграл определяется подынтегральным выражением, формой кривой интегрирования и указанием направления интегрирования. При изменении направления интегрирования криволинейный интеграл меняет знак.
2. Если участок кривой от точки до точки разбить точкой на две части и , то непосредственно из определения криволинейного интеграла II рода следует, что
.

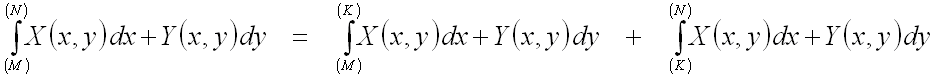Если криволинейный интеграл II рода вычисляется по замкнутой кривой , то его называют криволинейным интегралом II рода по замкнутому контуру и обозначают
.
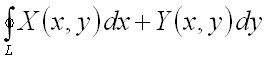При вычислении криволинейного интеграла II рода по замкнутому контуру необходимо учитывать направление обхода замкнутой кривой (против часовой стрелки или по часовой стрелке).

Вычисление криволинейного интеграла II рода

Если кривая задана уравнениями в параметрической форме:

где функции и непрерывны и имеют непрерывные производные и , и, кроме того, функции и также непрерывны как функции параметра на отрезке , то криволинейный интеграл II рода может быть вычислен по формуле:
,
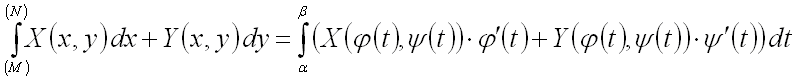где точкам и соответствуют значения и параметра .
Аналогично вычисляется криволинейный интеграл II рода по пространственной кривой , заданной уравнениями в параметрической форме .

Формула Грина

Пусть в плоскости дана ограниченная замкнутым контуром правильная область , причем ее проекцией на ось является отрезок , снизу область ограничена кривой , а сверху – кривой (в совокупности эти кривые составляют замкнутый контур ).
Пусть также в области заданы непрерывные функции и , имеющие непрерывные частные производные.
Тогда, если обход контура совершается против часовой стрелки, справедлива следующая формула:
.

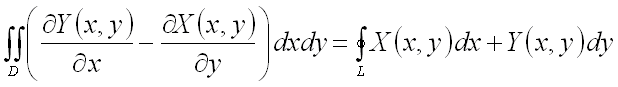Независимость криволинейного интеграла II рода от пути интегрирования

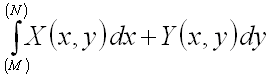Если для любых двух точек и криволинейный интеграл II рода не зависит от формы соединяющей их кривой, а зависит только от положения этих точек, то криволинейный интеграл II рода по любому замкнутому контуру равен нулю, т.е. .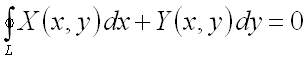
Справедливо и обратное утверждение: если криволинейный интеграл II рода по любому замкнутому контуру равен нулю, то этот криволинейный интеграл не зависит от формы кривой, соединяющей две любые точки, а зависит только от положения этих точек.
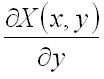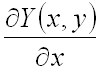Теорема. Пусть во всех точках некоторой области функции и вместе со своими частными производными и непрерывны. Тогда для того, чтобы криволинейный интеграл по любому замкнутому контуру , лежащему в области , был равен нулю, т.е. чтобы
,
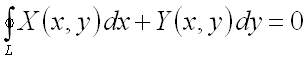необходимо и достаточно, чтобы во всех точках этой области выполнялось равенство
.

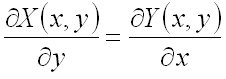Примеры решения задач

Пример 1. Вычислить криволинейный интеграл II рода 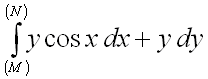вдоль кривой от точки до точки .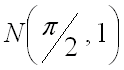

Решение.

Для вычисления интеграла представим кривую в параметрической форме, т.е. , где в качестве параметра возьмем переменную , тогда:

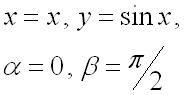
(значения и соответствуют значению параметра , т.е. в данном случае координаты , для точек и ).
Кроме того, необходимо найти и чтобы выразить и через выбранный параметр:
,
.
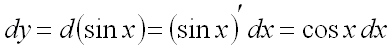Подставив все найденные выражения в формулу для вычисления криволинейного интеграла II рода
,
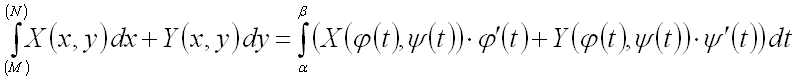получим:

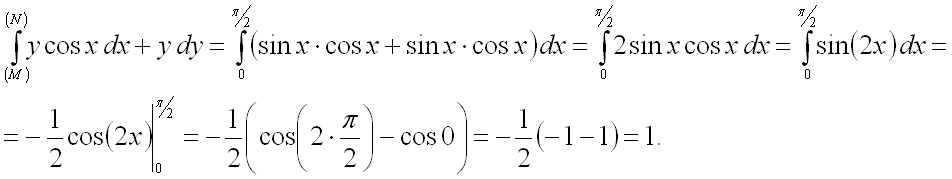
Ответ: 1.

Пример 2. Убедившись в независимости криволинейного интеграла II рода от пути интегрирования вычислить 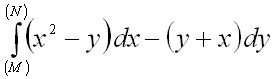от точки до точки .

Решение.

Для того чтобы доказать, что данный криволинейный интеграл II рода не зависит от пути интегрирования необходимо показать, что этот интеграл по любому замкнутому контуру равен нулю.
В свою очередь, согласно вышеприведенной теореме, для того, чтобы криволинейный интеграл по любому замкнутому контуру , лежащему в области , был равен нулю, т.е. 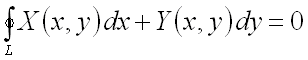, необходимо и достаточно, чтобы во всех точках этой области выполнялось равенство:
.
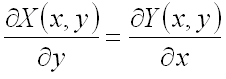Установим справедливость этого равенства. В нашем случае , а , тогда:

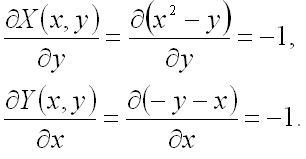
Поскольку установлено, что данный криволинейный интеграл II рода не зависит от пути интегрирования, то мы можем выбрать в качестве кривой интегрирования ломаную , где точка имеет координаты . Таким образом, ломаная составлена из двух прямолинейных участков, параллельных осям координат.
Далее воспользуемся вторым свойством криволинейных интегралов II рода:
.
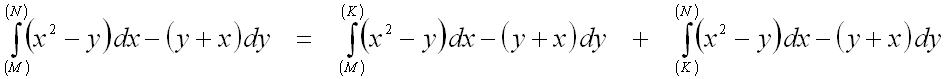Для вычисления первого слагаемого запишем в параметрической форме прямую . В качестве параметра возьмем переменную , а, учитывая, что прямая параллельна оси , т.е. вторая координата всегда остается неизменной и равной нулю, получим:

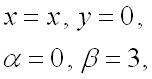
далее
.
Для вычисления второго слагаемого запишем в параметрической форме прямую . Так как прямая параллельна оси , т.е. первая координата всегда остается неизменной и равной 3, то в качестве параметра возьмем переменную , получим:

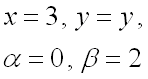
(значения и соответствуют значению параметра , т.е. в данном случае координаты , для точек и ), далее
.
Подставим все в исходную сумму:

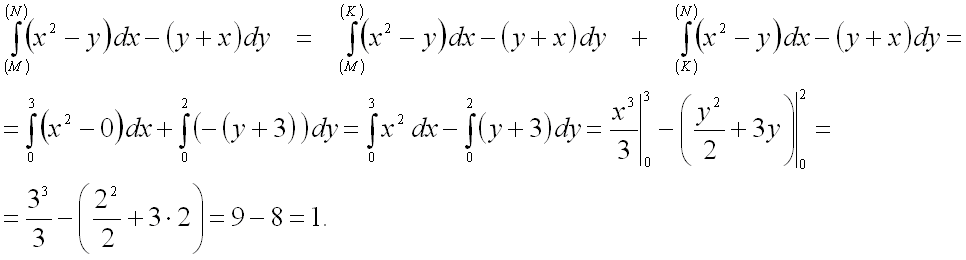
Ответ: 1.

Пример 3. Вычислить криволинейный интеграл II рода 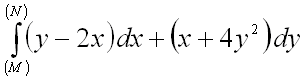от точки до точки по прямой .

Решение.

Для вычисления интеграла применим формулу:
,
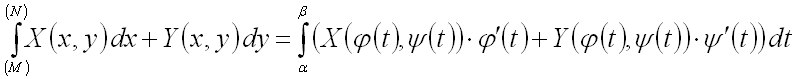где кривая задана уравнениями в параметрической форме, т.е. в виде пары уравнений (системы уравнений) , а точкам и соответствуют значения и параметра , кроме того, дифференциалы и заменены соответственно на и .
Чтобы воспользоваться этой формулой, сначала найдем уравнение кривой (в данном примере – прямой ). Для этого запишем уравнение прямой, проходящей через две заданные точки:
.
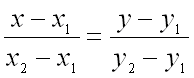Пусть – координаты точки , а – координаты точки , тогда получим следующее уравнение для прямой :

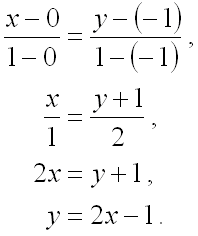
Далее для вычисления интеграла представим прямую в параметрической форме, т.е. в виде системы уравнений 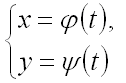, где в качестве параметра возьмем переменную , тогда:


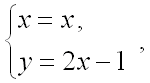
(значения и соответствуют значению параметра , т.е. в данном случае координаты , для точек и ).
Кроме того, необходимо найти и чтобы выразить и в исходной формуле через выбранный параметр. Учитывая, что в качестве параметра взята переменная , получим:
,
.
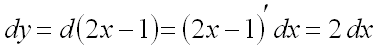Подставив все найденные выражения в формулу для вычисления криволинейного интеграла II рода, получим:

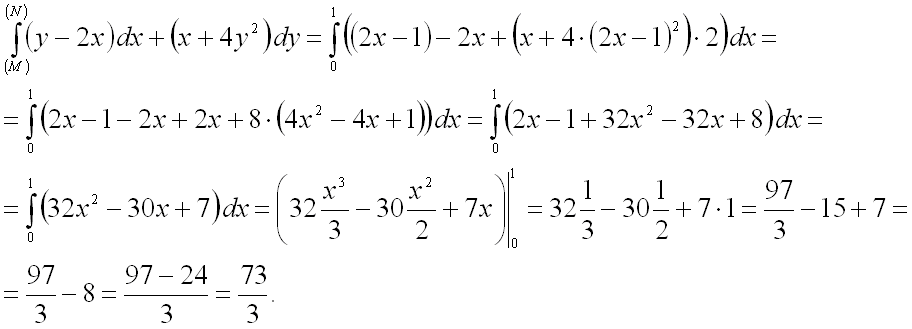
Ответ: .

Пример 4. Убедившись в независимости криволинейного интеграла II рода от пути интегрирования, вычислить 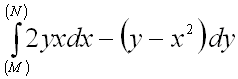от точки до точки .

Решение.

Для того чтобы доказать, что данный криволинейный интеграл II рода не зависит от пути интегрирования необходимо показать, что этот интеграл по любому замкнутому контуру равен нулю.
В свою очередь, известно, что для того, чтобы криволинейный интеграл по любому замкнутому контуру , лежащему в области , был равен нулю, т.е. 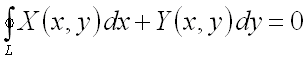, необходимо и достаточно, чтобы во всех точках этой области выполнялось равенство:
.
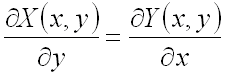Установим справедливость этого равенства. В нашем случае , а , тогда:

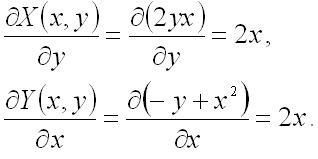
Поскольку установлено, что данный криволинейный интеграл II рода не зависит от пути интегрирования, то мы можем выбрать в качестве кривой интегрирования любую кривую. Возьмем ломаную , где точка имеет координаты , т.е. ломаная составлена из двух прямолинейных участков, параллельных осям координат. Такой выбор кривой интегрирования значительно упростит вычисления.
Далее воспользуемся формулой:
,
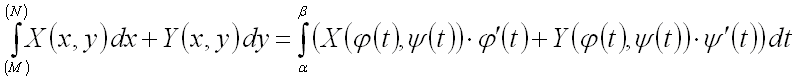а также вторым свойством криволинейных интегралов II рода:
.
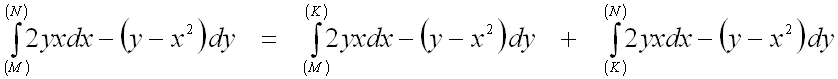Для вычисления первого слагаемого запишем в параметрической форме прямую , уравнение которой есть . В качестве параметра возьмем переменную , а, учитывая, что прямая параллельна оси , т.е. вторая координата всегда остается неизменной и равной 1, получим:

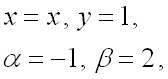
далее
.
Для вычисления второго слагаемого запишем в параметрической форме прямую , уравнение которой . Так как прямая параллельна оси , т.е. первая координата всегда остается неизменной и равной 2, то в качестве параметра возьмем переменную , получим:

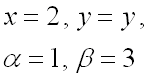
(значения и соответствуют значению параметра , т.е. в данном случае координаты , для точек и ), далее
.
В итоге для исходного интеграла получим:

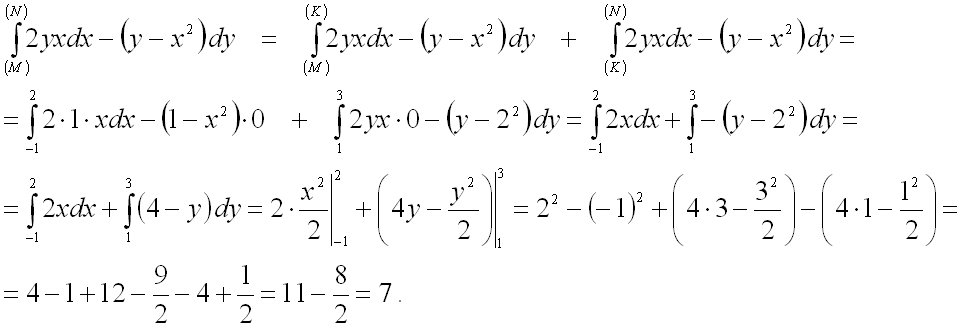
Ответ: .

Задания для самостоятельной работы

Вычислить криволинейный интеграл II рода:
1. 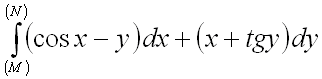от точки до точки 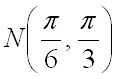по прямой .
Ответ: .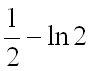
2. 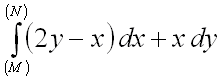от точки до точки по кривой .
Ответ: .
3. 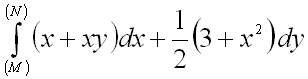от точки до точки :
a) по ломаной , где точка имеет координаты . Ответ: ;
b) по прямой . Ответ: ;
c) сравнить результаты, полученные в п.п. a) и b) и объяснить их совпадение.
4. 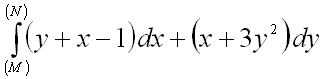от точки до точки :
a) по ломаной , где точка имеет координаты . Ответ: ;
b) по прямой . Ответ: ;
c) сравнить результаты, полученные в п.п. a) и b) и объяснить их совпадение.

Убедившись в независимости криволинейного интеграла II рода от пути интегрирования, вычислить:
5. 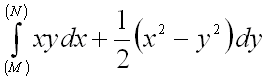от точки до точки .
Ответ: .
6. 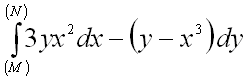от точки до точки .
Ответ: .
7. 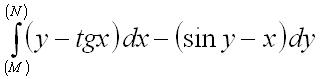от точки до точки .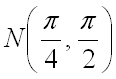
Ответ: .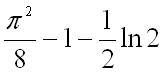
8. 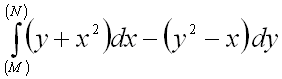от точки до точки .
Ответ: .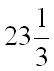

9. 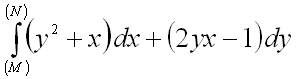от точки до точки .
Ответ: .
Вычислить криволинейный интеграл II рода:
10. 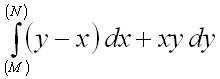от точки до точки по прямой .
Ответ: .