Экстремум функции двух переменных

Говорят, что функция имеет максимум в точке , т.е. при , если для всех точек , достаточно близких к точке и отличных от неё.

Говорят, что функция имеет минимум в точке , т.е. при , если для всех точек , достаточно близких к точке и отличных от неё.

Максимум и минимум функции называются экстремумами функции.

Теорема (необходимое условие экстремума функции двух переменных). Если функция достигает экстремума при , то каждая частная производная первого порядка от или обращается в нуль при этих значениях аргументов, или не существует.

Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку функция имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка является критической точкой функции , т.е.
,
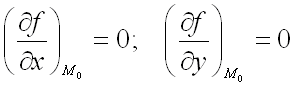тогда при :
1) имеет максимум, если дискриминант и , где ;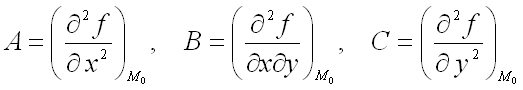
2) имеет минимум, если дискриминант и ;
3) не имеет ни минимума, ни максимума, если дискриминант ;
4) если , то экстремум может быть, а может и не быть (требуется дополнительное исследование).

Примеры решения задач

Пример 1. Исследовать на экстремум функцию .

Решение.

На первом шаге, в соответствие с достаточным условием экстремума функции двух переменных, найдем точки, удовлетворяющие условию:

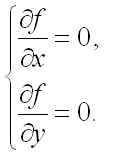
Частные производные первого порядка от функции равны:

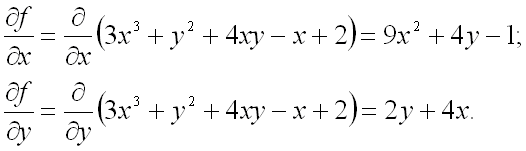
Приравняем их к нулю и решим систему уравнений:

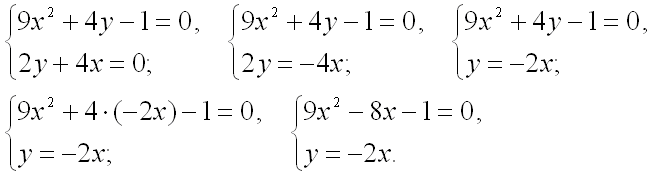
Выпишем отдельно первое уравнение системы и найдем его корни:

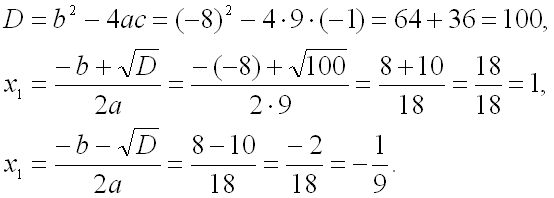
Подставим найденные значения переменной во второе уравнение системы:

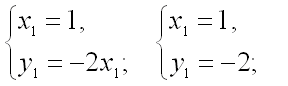и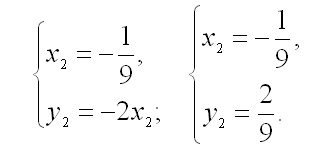

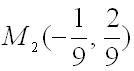Таким образом, получили две точки и , в которых будет продолжено исследование функции на экстремум.

На втором шаге найдем все вторые частные производные от функции :

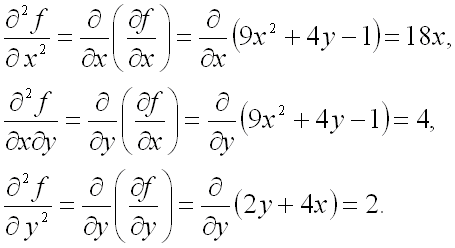
На третьем шаге для каждой из точек и 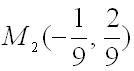установим наличие экстремума функции (для этого вычислим значения вторых производных и найдем знак дискриминанта в указанных точках).

1) Для точки :

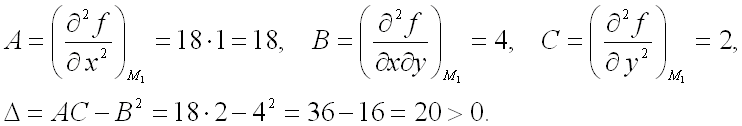
Так как дискриминант больше нуля и , то функция имеет минимум в точке :
.

2) Для точки :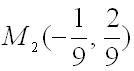

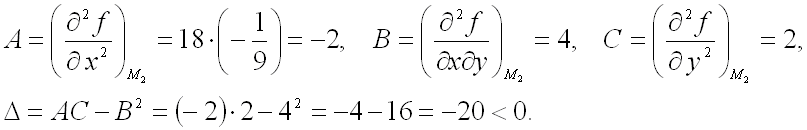
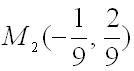Так как дискриминант меньше нуля, то функция не имеет в точке ни минимума, ни максимума.

Ответ: в точке функция имеет минимум.