Тема "Формула Бернулли. Теоремы Лапласа"

Формула Бернулли

Пусть производится независимых испытаний, в каждом из которых событие может появиться либо не появиться. Кроме того, будем предполагать, что вероятность события в каждом отдельном испытании одна и та же и равна (соответственно, вероятность того, что событие в каждом отдельном испытании не наступит, также постоянна и равна ).
Тогда вероятность того, что событие в независимых испытаниях произойдет ровно раз, равна
.
Данная формула называется формулой Бернулли.

Локальная теорема Лапласа

Использование формулы Бернулли при больших значениях требует выполнения арифметических действий над огромными числами, что обусловлено наличием факториалов в формуле для числа сочетаний. Поэтому, если число испытаний достаточно велико, то для нахождения вероятности появления события ровно раз применяют следующую теорему.
Теорема. Если вероятность появления события в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие появится в испытаниях ровно раз, приближенно равна (тем точнее, чем больше ) значению функции
.
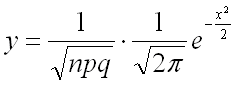Для положительных значений аргумента значения 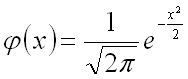функции приведены в специальной таблице. Для отрицательных значений аргумента пользуются той же таблицей и свойством четности функции , то есть .
Таким образом, вероятность того, что событие появится в испытаниях ровно раз, приближенно равна
,
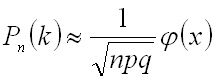где .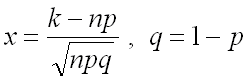

Интегральная теорема Лапласа

Теорема. Если вероятность появления события в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие появится в испытаниях от до раз, приближенно равна определенному интегралу
,
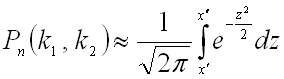где .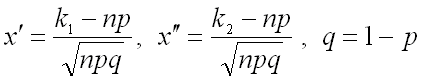
При решении задач, требующих применения интегральной теоремы Лапласа, используют специальную таблицу для интеграла 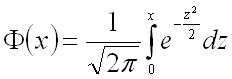. В ней приведены значения функции (которую называют функцией Лапласа) для . Если , то принимают . Для пользуются той же таблицей и свойством нечетности функции Лапласа, то есть .
Для того чтобы можно было пользоваться таблицей, преобразуем формулу из интегральной теоремы Лапласа:

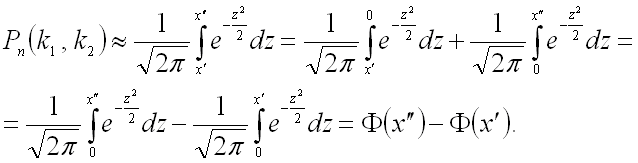
Таким образом, вероятность того, что событие появится в испытаниях от до раз, может быть вычислена по формуле
,
где .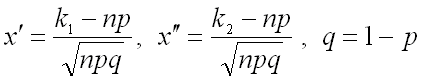

Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях

Обозначим через число появлений события в независимых испытаниях, в каждом из которых вероятность наступления этого события постоянна и равна (соответственно вероятность непоявления также постоянна и равна ).
Тогда, если изменяется от до , то дробь 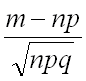изменяется от 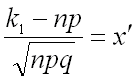до .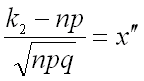
Следовательно, интегральную теорему Лапласа можно записать в виде:

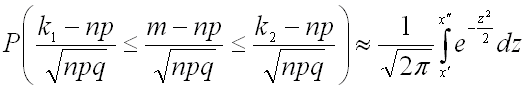
или
.
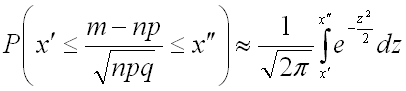Теперь поставим задачу найти вероятность того, что отклонение относительной частоты от постоянной вероятности не превышает заданного числа , то есть необходимо найти вероятность осуществления неравенства
.
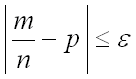Преобразуем последнее неравенство, заменив знак модуля двойным неравенством и затем приведя к общему знаменателю:
,
.
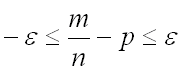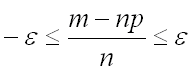Умножим все неравенство на выражение :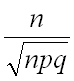
.
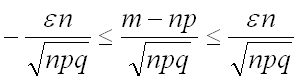Теперь, если обозначить 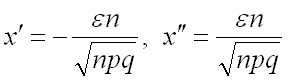, то преобразованная теорема Лапласа может быть записана в виде:

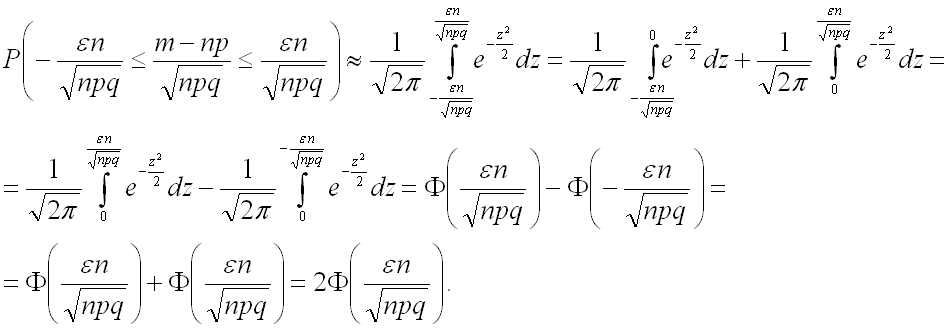
Заменив двойное неравенство в левой части последней формулы на исходное выражение 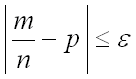, окончательно получим:
.
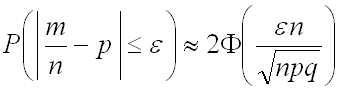Вывод: вероятность того, что отклонение относительной частоты от постоянной вероятности не превысит заданного числа , приближенно равна удвоенной функции Лапласа с аргументом 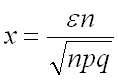.